Utilitarismo vs "paretianismo": una descripción gráfica

Utilitarismo y paretianismo (no volveré a marcarlo en lo sucesivo) son dos criterios de aceptabilidad de una determinada medida. Pero nada mejor para entenderlos y compararlos que la siguiente gráfica (extraída de un libro de Joseph Heath que no viene al caso):

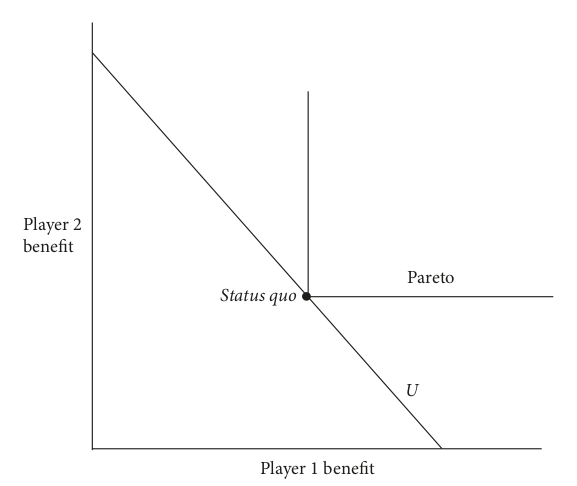
Creo que lo dice todo. Pero para que no haya lugar a dudas, lo que sigue.

El cuadrante que muestra la figura muestra potenciales estados del mundo. Sus coordenadas en los ejes X e Y muestran la utilidad de dicho estado para los jugadores 1 y 2. La situación actual está representada por el punto grueso (llámese $x_0$), que determina utilidades $U_1(x_0)$ y $U_2(x_0)$ para los jugadores 1 y 2.

La línea oblicua es aquella que mantiene constante la suma $U_1(x) + U_2(x)$ (e igual a $U_1(x_0) + U_2(x_0) = U_0$). Desde una perspectiva utilitarista, cualquier $x$ a la derecha de dicha línea sería aceptable porque en tal caso

$$U_1(x) + U_2(x) > U_0,$$

es decir, se ganaría en conjunto por más que pueda suceder que $U_1(x) < U_1(x_0)$ o que $U_2(x) < U_2(x_0)$, es decir, que alguien salga perdiendo.

El paretianismo es más estricto y solo acepta $x$ si $U_i(x) \ge U_i(x_0)$ para cada $i$. Es decir, si la nueva medida se encuentra en el subcuadrante apoyado en $x_0$ que aparecen en la figura.

Ejercicio: ¿Cuál sería la geometría del principio max-min?